二阶sdm为什么会出现稳定性问题？需要达到一个什么样的功能？

我们在上一个文章中设计了一个二阶的sdm，如下图，

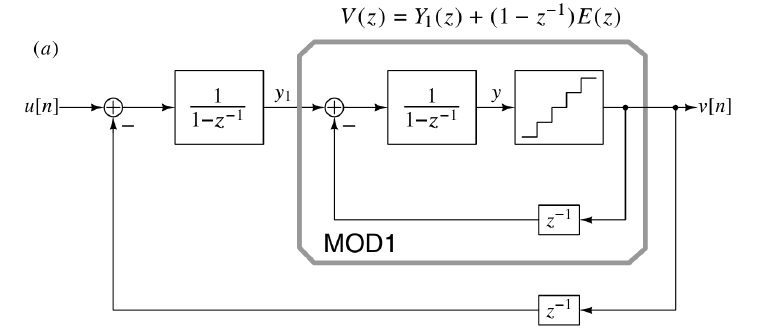
我们根据这个二阶sdm搭建了一个simulink模型进行仿真，输入是分子和分母，我们发现，当小数靠近0的时候（例如分子为1，分母为16），counter的数据会无限减小，导致mod1的输出一直为1，系统进行一个不收敛的状态。

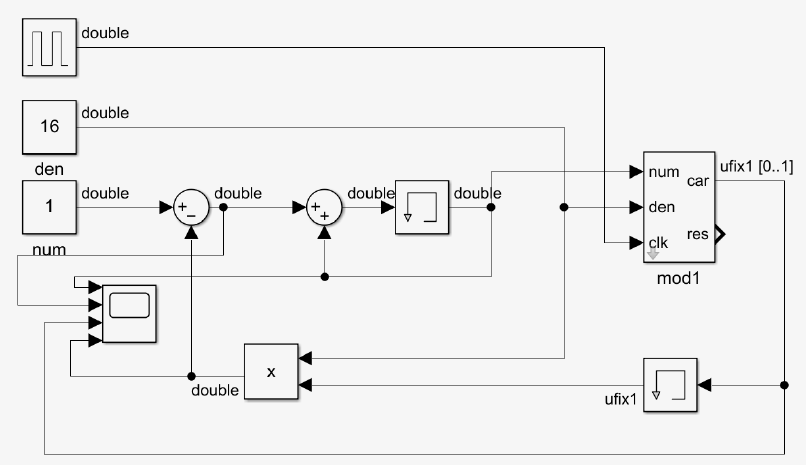
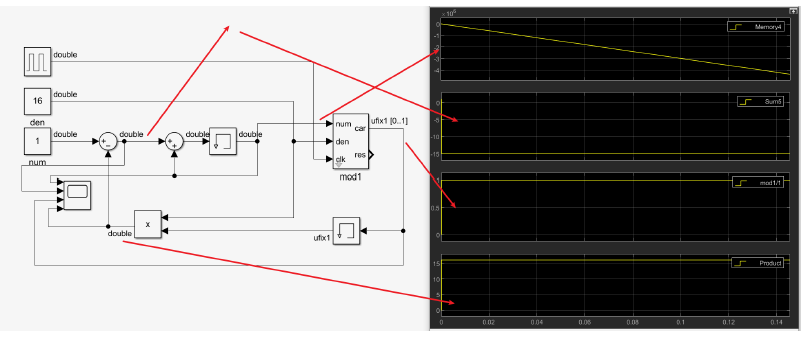
仿真结果如下，体现在mod1的分子输入会一直大于分母，因此系统一直发散。

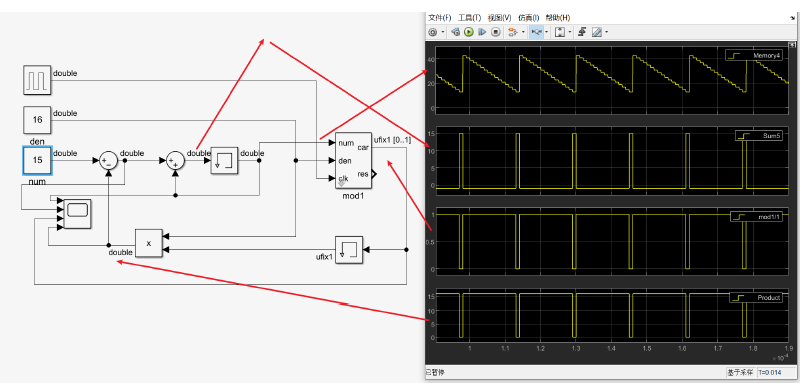
但小数接近1的时候却并不会出现这样的问题，以下是15/16的仿真结果，至少会保证在一个合适的范围内，在使用verilog实现时，可以增加位宽实现

这是为什么呢？我们当初分析时都没有出现这种问题，原因是我们在对量化器做模型时，直接对量化器线性化了，而量化器的模型实际上是非线性的。

量化器的模型应该为V(n) = sign(x(n))

而我们直接线性化为V(z) = X(z) +E(z)

❓ 高阶sdm的稳定性问题如何解决？

上面提到的高阶sdm实际上是一次性对量化噪声进行高阶整形。既然直接对量化噪声使用高阶整形会产生稳定性问题，那么，应该怎么办呢？其实，我们是不是可以给他多来几次整形呢，就像在PLL设计中常见的，一个buffer推不动，我就一级一级推。

对，那我们可以把一阶的量化噪声再整形一次，这样量化噪声是不是会更小，并且稳定性问题也能同样解决。

所以，我们完全可以将整形一次的量化噪声再送到一个一阶sdm中，如下图：

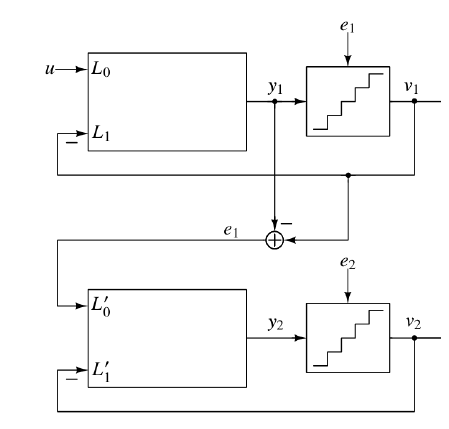
对于量化噪声的求解，只需要将量化器的输出减去量化器的输入即可，也就是图中的L0’的位置。但是，这会产生一个问题，输出应该怎么选择，v1还是v2呢。这个时候，又需要观察一下系统函数。

如果看过我写的上一篇文章，就可以知道，

V1（z) = STF1(z) U(z) + NTF1(z)E1(z)

同样的，

V2（z) = STF2(z)E1(z) + NTF2(z) E2(z)

由于我们想要得到一个平均值是与输入相关的函数，最终输出，我们可以设置合适的STF函数，将E1（z)消除。因此，我们可以在V1（z)后面加一个系统，如下图所示

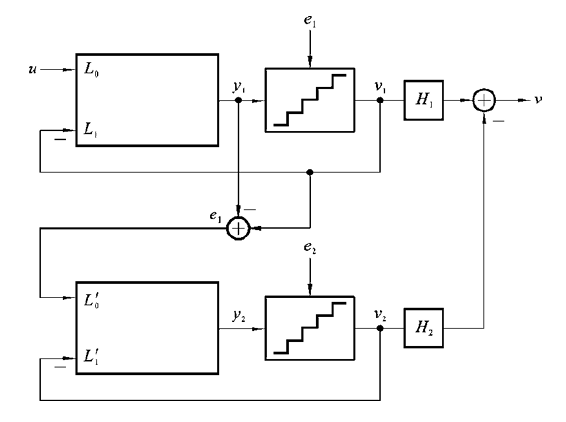
只需要满足H1(z) NTF1(z) = H2(z) STF2(z)就可以消除掉V1(Z)

当H1(z)=1的时候，就变成

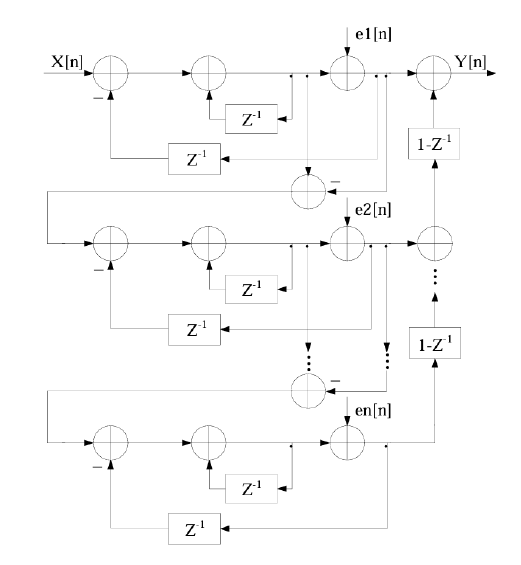
最终，MASH 1-1-1的sdm效果可以和三阶sdm效果一致。

我们对MASH 1-1-1进行simulink仿真

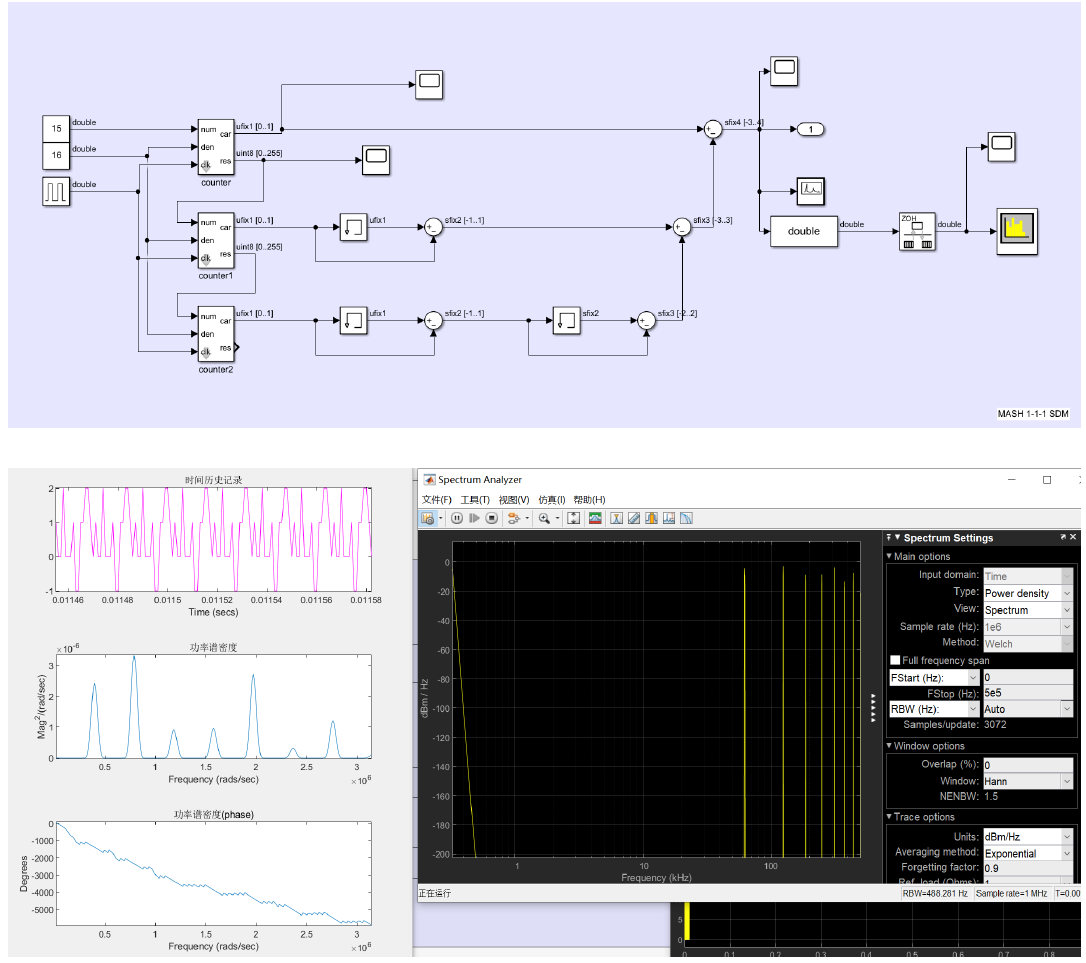
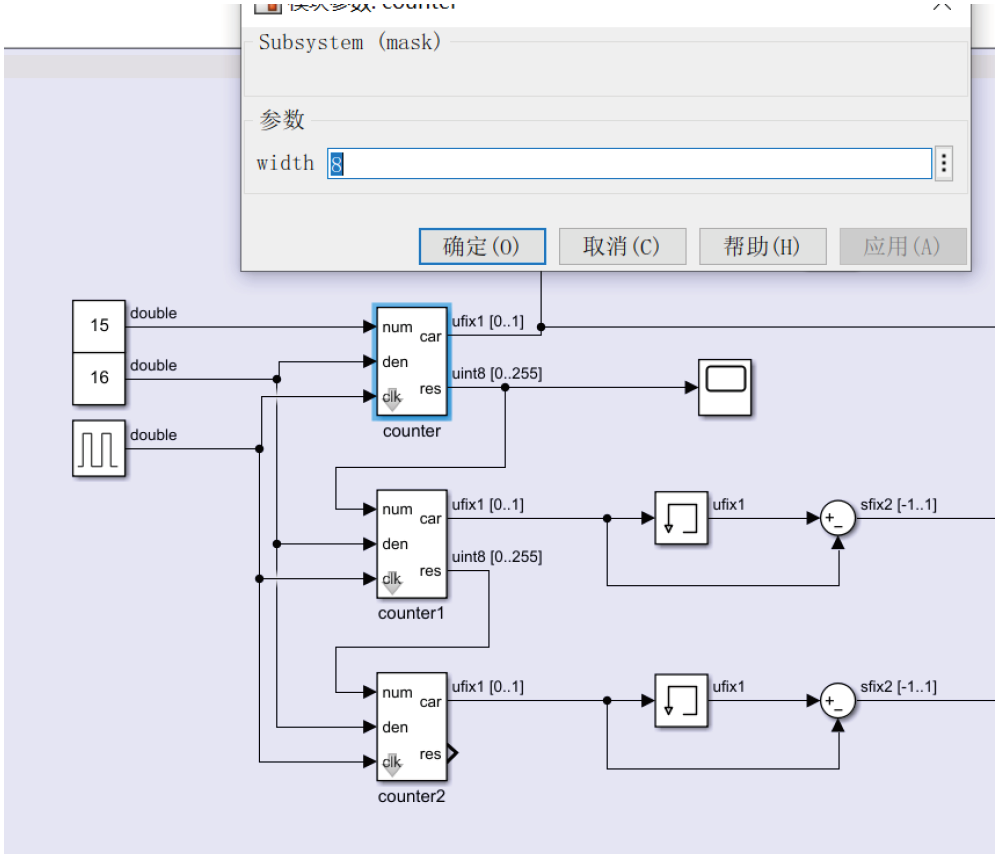
由于要贴合PLL设计，这里使用clk作为trigger，后面搭建PLL的模型，可以使用MMD的输出clk作为sdm的clk，并且使用定点数设计，此外，counter还设置了参数，可以直接设置bit数，更接近我们实际的设计。

💡 为什么MASH 1-1-1的输出范围是【-3，4】？

从我们的simulink模型看，mash 1-1-1在输出时经历了很多减法，第三级经过一次差分范围后是[-1,1],经过第二次差分后范围是[-2,2]，送往第二级，是[-2,2]与[-1,1]之间求差，范围是[-3,3]，再送到第一级，是[-3,3]和[0,1]求差，范围结果是[-3,4]。

这在simulink模型中都是标注了的。比如ufix1就是无符号数定点数1bit，sfix2就是有符号数2bit。

sdm的simulink模型在我的微信公众号输入sdm可以下载。公众号是gh_c29cca7839c6，朝望。我的主页有二维码，需要的话可以关注一下。

📎 遗留问题

PLL中的sdm还会增加dither减小spur，这个是如何实现的呢？

我们下一篇文章再见

参考文献：UNDERSTANDING DELTA-SIGMA DATA CONVERTERS -Tariq Samad