✳ sdm需要达到一个什么样的功能？

从出发点开始，我上一篇文章讲了，其实sdm的出现是为了解决两个问题：

一，产生一组序列，这组序列的平均值为输入的某个小数。

二，噪声整形，将这串序列的量化噪声尽量分布在高频，以此在PLL中才能被最大限度的滤除。

那么，这两个应该如何去设计。

❓ 平均值为输出的整数序列如何产生？

说到平均值，我们第一时间想到的是求和再除。

用式子表示就是 ( v[1] + v[2] + … + v[n]）/n = Fra

其中Fra是我们想要的小数，v[1],v[n]分别是我们想要的序列的第一个值和第n个值。

但是，我们的Fra是一个输入，v[n]才是输出。因此，可以把上面的式子对换一下

v[1] + v[2] + … + v[n] = n * Fra 因此

v[1] = 1*Fra

v[2] = 2*Fra - v[1]

v[n] = n*Fra - v[1] -… -v[n-1]

但是，我们的序列v[n]是有一个前提的，v[n]是必须是一个整数，而1*Fra明显是一个小数，我们这个时候就会引入一个量化器，将小数量化成整数，但是引入了量化噪声。所以上面的式子变成

v[1] =Q{ 1*Fra}

v[2] = Q{2*Fra - v[1]}

v[n] = Q{n*Fra - v[1] -… -v[n-1]}

其中Q{}表示对括号中的式子进行量化。

如果把输入Fra也转成一个固定的小数序列u[n]，那么上面的式子就是

v[n] = Q {y[n]}，其中y[n] = y[n-1] + u[n]

具体推导如下

v[1] = Q{ u[1] }

v[2] = Q{ u[1] + u[2] -v[1] }

v[n] = Q{ u[1] + u[2] + … u[n] - v[1] -v[n-1] }

引入一个y[n] = y[n-1] - v[n-1] + u[n]

v[n] =Q{ y[n] }

这个时候，这个平均值为输入的整数序列的系统就初具雏形了。把这个系统画出来，你会发现，这就是一个一阶SDM！下面的图来自文献1

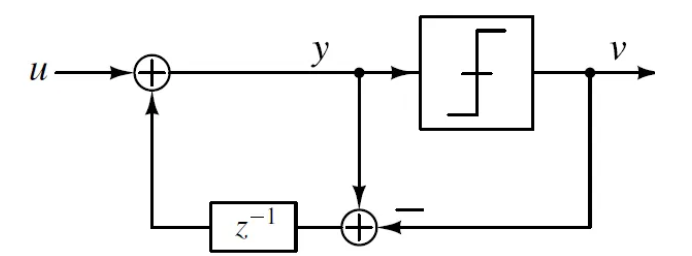
那接下来，就是怎么把这个系统的噪声整形成我们想要的样子。

💡 如何将噪声整形成我们希望的样子呢？

首先，我们先分析上面那个一阶SDM的量化噪声是什么样子。

对于量化器来说，假设量化噪声是e[n]，那么量化器的输出则为v[n] = y[n] - e[n](文献中是v[n]= y[n] +e[n]，其实不会影响最终的噪声形状，都没有错)

我们想要得到的一个式子是输入u[n]和输出v[n],量化噪声e[n]的关系，这样就可以知道噪声是什么样子了。

经过推导，可以得出v[n] = u[n] +e[n-1] -e[n]。

以下是推导，觉得麻烦可以跳过。

在整个系统中，y[n] = y[n-1] - v[n-1] + u[n] ,

y[n] = y[n-1] - v[n-1] + u[n] =v[n] + e[n]

v[n-1] - v[n-1] +e[n-1] +u[n] = v[n] + e[n]

v[n] = u[n] +e[n-1] -e[n]

这个结果跟文献中的v[n] = u[n] + e[n] - e[n-1]不一致，原因是文献中量化器的定义是v[n] = y[n] + e[n]，其实并不影响噪声的形状。

将这个转为z变换，可以得到V[Z] = U[Z] - (1-1/z )E[Z]

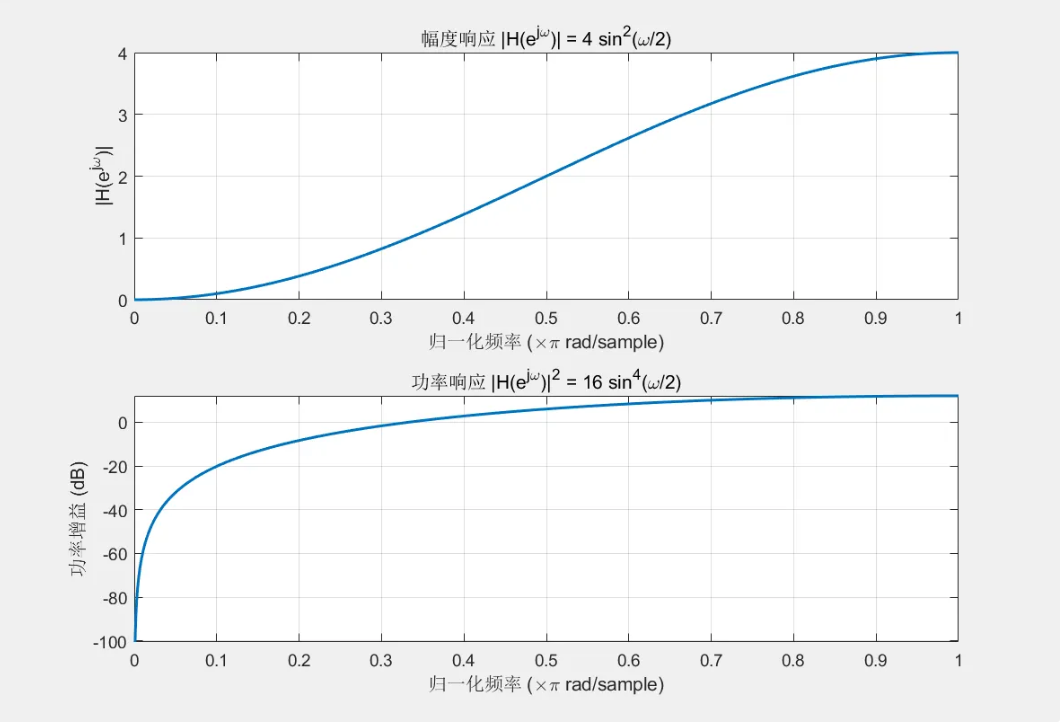
我们可以很清晰的看到，量化噪声E[z]其实是被1-1/z这个系统整形过的，我们突然发现，原来一阶的SDM也有整形功能，形状是什么样子呢，形状就是1-1/z，文献中管这个叫做噪声传递函数（NTF)。我们关注功率谱，所以看一下（1-1/z)²的形状是什么样子，是一个高通的形状。

也就是说，一阶的SDM其实也有将量化噪声推向高频的功能！

如果sdm中的量化噪声是白噪声的话，被整形的效果可以看到

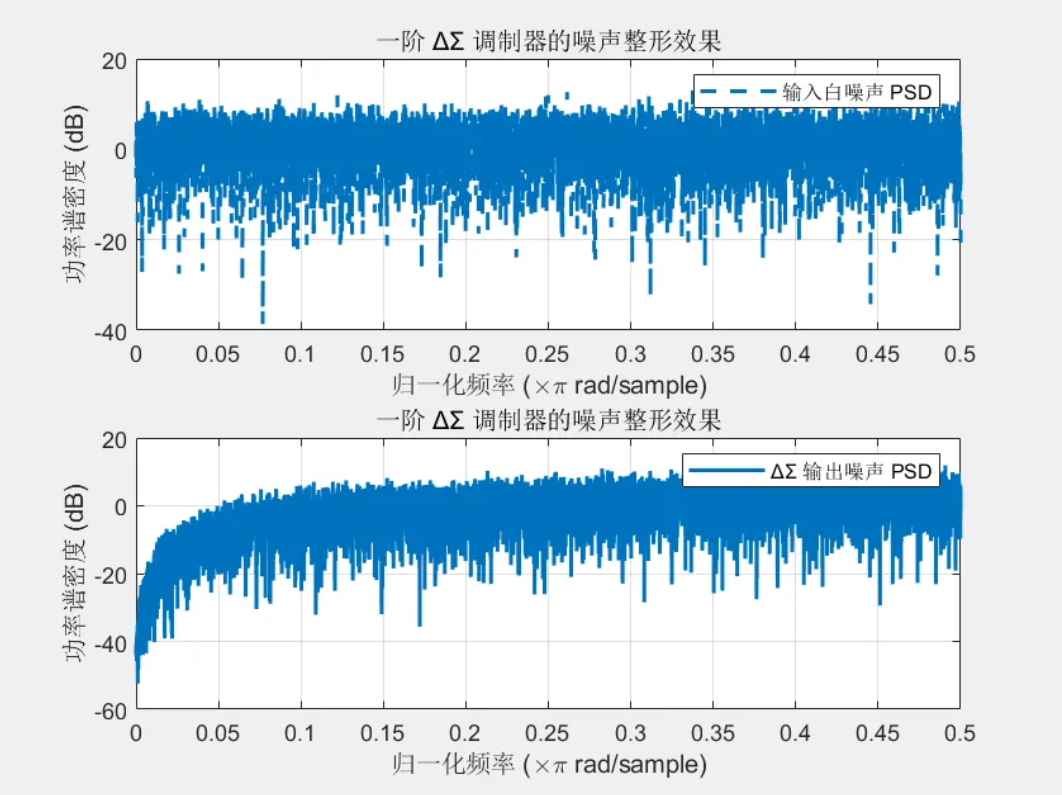
回过头来想想，为什么我们在实现平均这件事上，顺便做了一个噪声整形呢？是一个巧合吗？其实不是，我们在实现平均的时候，载波其实是固定的，所以噪声在接近0频率的时候必然会比较低。

虽然一阶SDM具有噪声整形功能，但是整形效果没有达到我们的预期。

如果我们想要将噪声整形到更高频呢，如何做？在解答这个问题的时候，我先提一个问题，我们噪声整形，实际上是想噪声在0Hz附近衰减，这个系统应该怎么做？这个系统的零点和极点会怎么分布？

首先在0Hz最小，肯定会有一个z=1(w=0)的零点；z-1这个系统是一个非因果系统，如果要得到一个因果系统，那z-1/z是一个很好的选择。这个时候，你会发现，一阶SDM的噪声传递函数就是z-1/z，然后，怎么让这个传递函数更好的衰减呢？是不是给这个系统函数加零点？对，加哪里？当然是加在z=1的地方更好，所以，想要更好的衰减，噪声传递函数是 （z-1)^L/z，L=2，3。但是由于零点增加了，系统会不稳定，因此，此时，也需要增加极点。最终噪声传递函数是

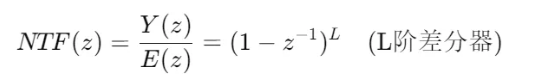
你会发现，这个跟L阶sdm的噪声传递函数是一样的。

下图是L=1,2,3的幅频对比图，L越大，低频抑制效果越好

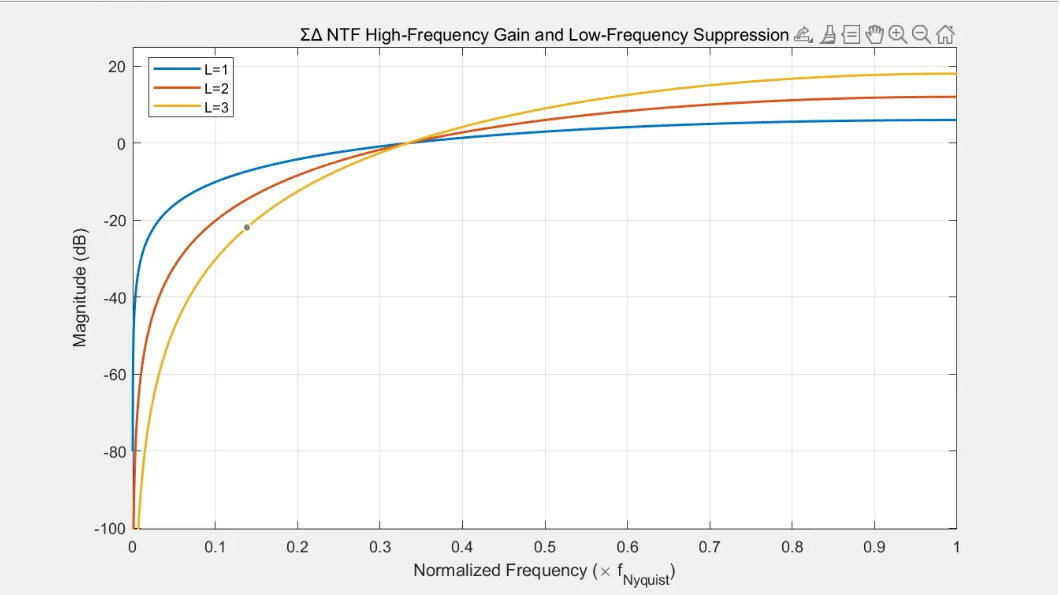
🎨高阶sdm是如何设计的？

我们想要噪声整形的效果更好，只需要将L加大

当L=2时，那么系统函数变为

V[Z] = U[Z] + (1-1/z )²E[Z] 此时，系统框图如下图所示

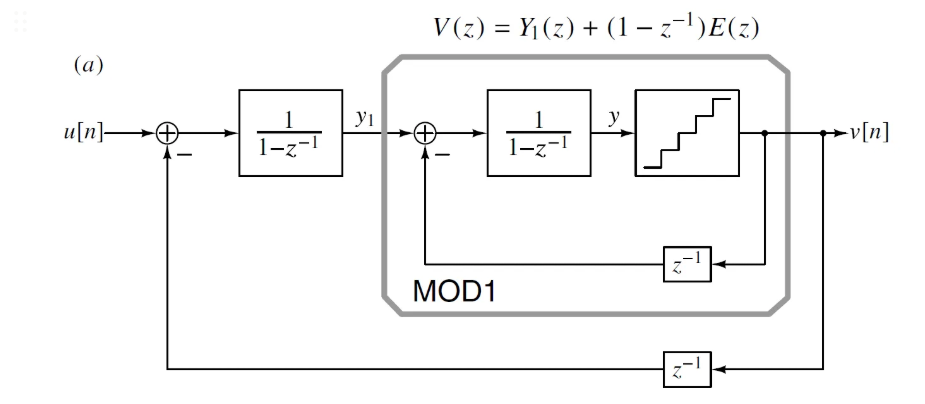
你会发现，这是一个二阶的SDM，这个时候，你又设计了一个整形能力更好的二阶SDM，如果你想设计一个三阶的SDM，同理，增加L到3。

🥎实际电路中的设计

在实际电路中，积分器的输出会随着n的增长而增长，而积分器（verilog中是counter）会有最大的积分限制。这个问题可以通过简单的将积分器移动到环路中避免。如图所示

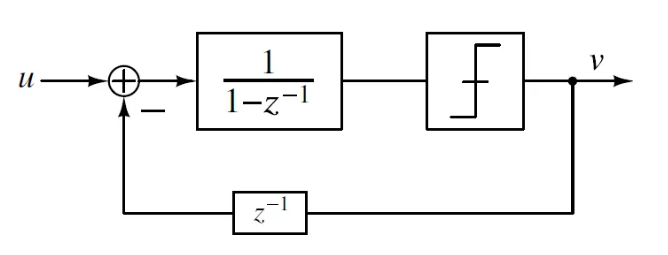
但是，传递函数从V[Z] = U[Z] - (1-1/z )E[Z]变为V[Z] = (1/z)U[Z] + (1-1/z)E(Z)，但是并不影响功能。同理，二阶SDM也变为V[Z] = (1/z)U[Z] + (1-1/z)²E(Z)

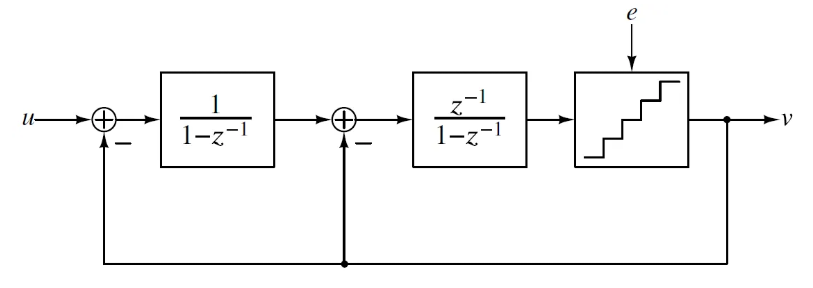
📎 遗留问题

实际上，这种高阶的SDM会存在稳定性问题，所以才会有人提出MASH结构的SDM去解决稳定性问题

为什么会存在稳定性问题呢？MASH结构的SDM是如何提出来的呢？

我们下一篇文章再见

参考文献：UNDERSTANDING DELTA-SIGMA DATA CONVERTERS -Tariq Samad