大家都知道，一个典型的PLL是由VCO（压控振荡器），PFD CP（鉴频鉴相器和电荷泵），LPF（环路滤波器）组成。为什么会由这几个部分构成的呢？

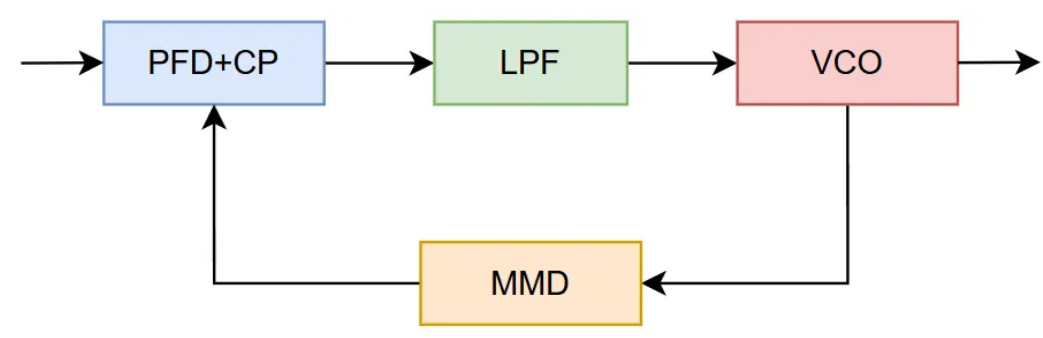
首先，需要明确PLL的应用场景是什么？

①频率合成（Frequency Synthesis）。也就是产生一个我想要的稳定频率，并且这个信号的噪声需要满足我的标准。比如收发机中常见的2.4GHz

②时钟同步（Clock synchronization）。输出信号需要与输入的时钟进行同步，保证一定的相位关系。例如FPGA中常用的用一个PLL产生多个同相位的时钟。

③去抖（jitter cleaning）。类似于将PLL充当一个低通滤波器（带宽非常低），将输入信号的噪声绝大部分都滤除掉。

④时钟恢复（clock/data recovery, CDR）。主要应用在串行通信中，需要重数字信号中提取出他的时钟信号。

在本文中，暂时只考虑频率合成这个应用场景。

既然是频率合成，那么我们需要考虑第一个的问题是，什么电路能产生一个频率信号？

什么电路能产生一个频率信号？

①压控振荡器，比如LC-VCO，RC-VCO，Ring-VCO

②晶体振荡器

③mems振荡器等

简单对比一下这几个电路。这里的优差只是一个相对的概念

这里只是简单的对比，比如频率范围，VCO也可以做THz级别的，但晶振目前没有查到能做GHz级别的。

通过这个简单的对比，可以知道，想要一个频率可调，频率范围较大的频率输出，压控振荡器才是一个很好的选择。

假如说你的要求是固定几个频率，并且输出频率比较低，能不能使用晶体振荡器呢？其实也很难直接使用晶体振荡器。因为晶振的频率往往是标准频率点，比如10MHz，20MHz等等。市面上很少能购买到定制频率的晶振，有的商家写的是可任意频率的晶振，其实里面还是配置了一个PLL。

既然选定了一个产生频率信号的电路，那么

VCO能不能直接作为一个频率合成器呢？

我们看看VCO的频率表达式，fvco= f0 + vtune * Kvco

其中，f0是中心频率，vtune是vco的输入，kvco是vco的增益。

这在理论上貌似可以实现，只需要控制我的vtune，让输出频率与我设置的一样，并且保证VCO的噪声要求满足我的指标就可以。但是在实际芯片设计中，需要考虑工艺、温度、电压（PVT）的影响。你在设计VCO时，在你流片测试前，你都无法准确知道你设计的VCO是工作在哪个频率，并且随着温度，电压的变化，VCO的频率也会变化。即便你设计了一个很准的vtune值，你也不能保证，VCO输出的频率是你想要的那个频率。

因此，VCO直接作为一个频率合成器不太现实。

如果想要稳定的输出，应该怎么做呢？

这个问题，是在有干扰、参数变化时仍能让系统稳定工作，其实属于自动控制学的范畴。

那么，自动控制理论中有哪些呢，什么可以应用在控制VCO呢

常见的自动控制有以下：

①PID（比例、积分、微分）控制

②Lead-Lag（超前-滞后）控制

③Kalman Filter（卡尔曼滤波）等等

可以知道的是，PLL选择了PID作为控制VCO的自动算法。至于为什么选择这个算法，有部分原因是简单可靠，具体还需要大幅度展开，在此不做深究。

由于自动控制理论近些年也在快速发展，或许还可以采用其他控制算法实现PLL，开辟新的架构也说不定。

什么是PID算法？

简单来说，就是测量输出信号于基准的误差，通过比例+积分+微分三个调节去让受控部分的输出稳定。

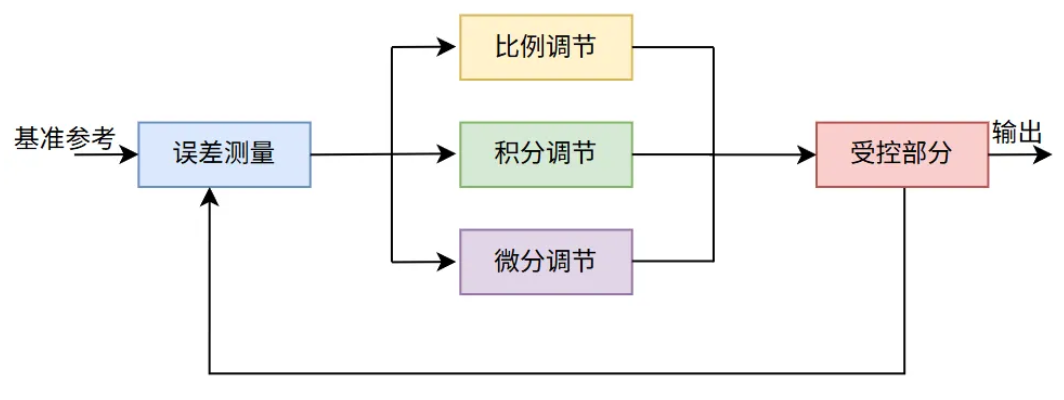
举个例子，假如受控部分是VCO，初始频率为2.2GHz，基准参考是2.4GHz。

比例调节：

测量误差为0.2GHz，假设比例积分为0.5，那么就要控制VCO提高频率，提高的频率为0.2×0.5=0.1GHz，其中0.2为误差，0.5为比例积分，那么经过这次调节，VCO频率变为2.2+0.1=2.3GHz。

第二次测量误差为0.1GHz，那么VCO频率变为2.3+0.1×0.5=2.35GHz

以此类推，最终稳定在2.4GHz，此时误差会缩小为0。

但是，这是在理想的情况下，通常现实中的模块都会有误差，比如，假设每次控制VCO，你想让VCO增加1GHz，但由于PVT的影响，会比预期少0.1GHz，结果只增加了0.9GHz，这个时候，会发生什么情况呢？重新考虑上面的情况

测量误差为0.2GHz，提高的频率为0.2×0.5-0.1=0GHz，那么VCO的频率变为2.2GHz

此时，VCO会一直稳定在2.2GHz，距离目标频率2.4GHz永远会有0.2GHz的差值，这个就是稳态误差。假如这个误差在能接受的情况下，那么也不需要处理。如果想要消除稳态误差，如何解决？增加积分路径。

积分调节

在增加积分调节后，假设积分调节的系数为0.1，重新考虑上面的情况。

测量误差为0.2GHz，比例调节为0GHz，积分调节为0.2x0.1=0.02GHz（积分器的初始值设置为0），总的调节为0+0.02=0.02GHz，那么VCO的频率为2.22GHz

第二次测量误差为0.18GHz，比例调节为0.18*0.5-0.1=-0.01GHz由于是负值，实际上是0，也就是比例调节已经调整不了了，积分调节（0.2+0.18)x0.1=0.038GHz，总的调节为0+0.038GHz，那么VCO的频率为2.22+0.038=2.258GHz

最终测量的误差会为0，导致积分不再增加，从而消除了稳态误差。

那微分调节是为了做什么的呢？

微分调节

在整个自动控制系统中，实际上有可能会波动很多次才逐渐稳定。比如目标2.4GHz，初始VCO频率为2GHz，误差为0.4GHz，可能PVT的影响，实际上给VCO增加了0.5GHz，那么VCO频率变为2.5GHz，那么VCO比目标频率高了0.1GHz，这个过程类似于震荡，然后趋于稳定。

如何减小这个震荡，让系统一次就趋于稳定呢，这个时候，只需要增加一个微分调节就可以了，在连续系统中，就是求导，在离散系统中，就是求差。

这个微分调节部分在趋于稳定的过程，会与比例调节的符号相反。比如第一次的误差为0.4GHz，第二次的误差为0.2GHz，此时微分调节是-0.2。当然，如果比例调节和积分调节的系数设置的好的话，其实也可以不需要微分调节。

这里给出一个gif图，让大家更好感受PID的功能。（此图是网上找的，侵删）

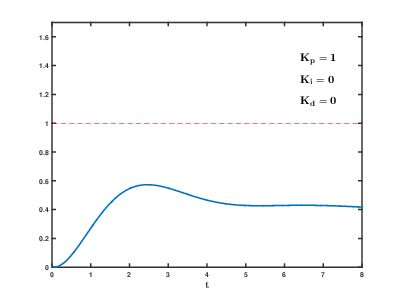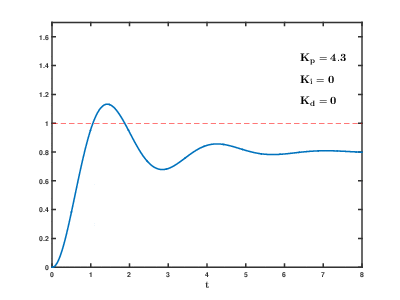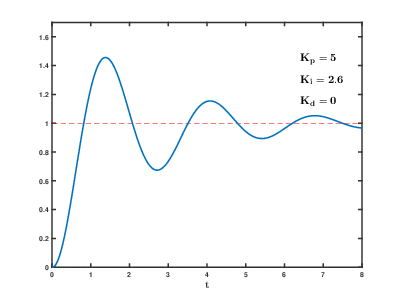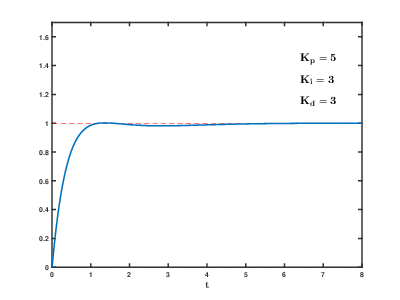
图中的Kp，Ki，Kd分别指的是比例，积分，微分的系数，当Ki=0，意味着系统未加入积分调节，同理，当Kd=0时，意味着系统未加入积分调节。

横轴为时间，纵轴是系统输出，红色虚线就是目标，也就是1，相当于我们上面的VCO目标频率2.4GHz。从图中我们可以提取出这些信息：

①当只有比例调节时，系统输出稳定≠1，存在稳态误差。并且Kp越大，系统响应越快，稳定需要的时间越少（在PLL中，也就是带宽大）。

②增加积分调节后，系统输出稳定=1，但Ki越大，震荡越大。

③增加微分调节后，系统震荡趋于消失。

在此，我们的频率合成器貌似已经有一个雏形了，具体就是如何实现了。但是其实，还有一个问题，既然我们的频率合成器想要一个频率稳定的输出，为什么要用锁相环（PLL），而不用锁频环(FLL)呢？

频率合成器为什么用锁相环而不用锁频环

首先，锁相环和锁频环的区别是什么？

在于测量输出与基准的误差时，一个是测量相位，一个是测量频率。

假如使用锁频环，那么输出的信号是sin(2πf+φ(t))，f是一个稳定的值，但是相位φ(t)是不确定的，可能会小，也可能会变化很大。这个会影响什么呢？

会影响输出信号的瞬态频率，sin(wt+φ(t))只能保证平均频率是f，那么瞬态频率是什么，是相位的导数，也就是d(φ(t))/dt，如果相位是一个不确定的值，那么瞬态频率也会不确定。

这里需要明白的是，相位的导数是频率，频率的积分是相位。

而我们在实现频率合成器时，是希望输出的瞬态频率稳定的，所以频率合成器应该使用锁相环实现，而不是锁频环实现。

接下来就终于步入正题了，如何实现锁相环？

如何实现锁相环？

我们回过头去看一下PID的环路图，主要有基准参考，误差测量，受控部分，PID调节这几个部分。

①首先考虑受控部分，那么就是VCO，是压控振荡器（也有电流控制的振荡器），所以误差测量的相位差需要转为电压信号，这样才能控制VCO，同理，如果是电流控制的振荡器，就需要转为电流信号，现在还有数字锁相环，那么需要转为数字信号。

②基准参考。基准参考是需要非常准确的，并且有频率和相位的信息。由于需要把相位信号转为一个电压信号，所以基准参考可以用一个电压信号做为基准，当然，如何将这个电压信号与频率和相位挂钩是一件比较难的事情，所以目前这样做的人比较少，文献1中就有这样做时钟发生器的，不过产生的是一个锯齿波。

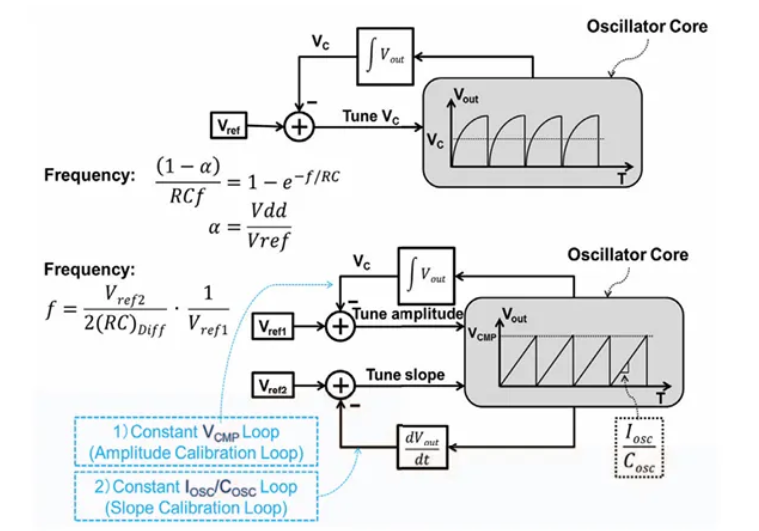
既然需要频率和相位的信号，那么外部给的一个准的信号是一个很简单的实现，比如晶振，现在大多数PLL就是这么做的。

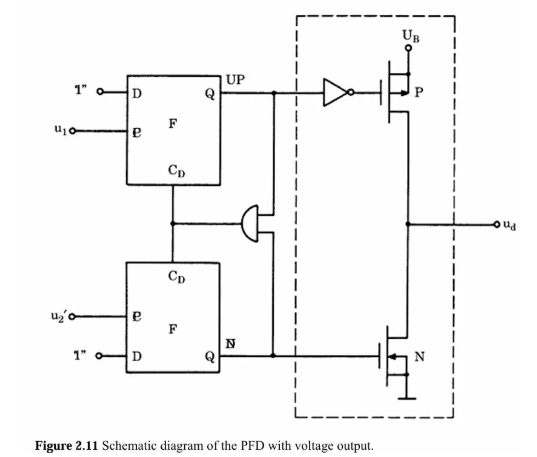
③误差测量。就是需要把误差信息转为电压信号，最直接的就是phase-to-voltage Converter，有很多种实现方法，比如异或门相位检测器，边沿触发的JK触发器，以及现在常用的PFD，下面给出电压输出的PFD，其他电路图，大家有兴趣的话，可以看文献2。当然现在PLL常用的是PFD电流输出的，为什么呢？因为电压输出的PFD无法对微小的相位误差做出响应。具体需要后面重新开一篇讲。

④PID调节部分。这部分可以认为是环路滤波器的一部分。PID其实是对输出的电压或者电流，做一个乘法，积分，和加法。很自然的，乘法和积分，加法都可以用运算放大器实现。主要实现的方法有无源lead-lag filters（超前滞后滤波器），有源lead-lag filters，有源PI滤波器。下面给出有源PI滤波器的电路图。对其他滤波器有兴趣的，可以看文献2（文献可下载）。

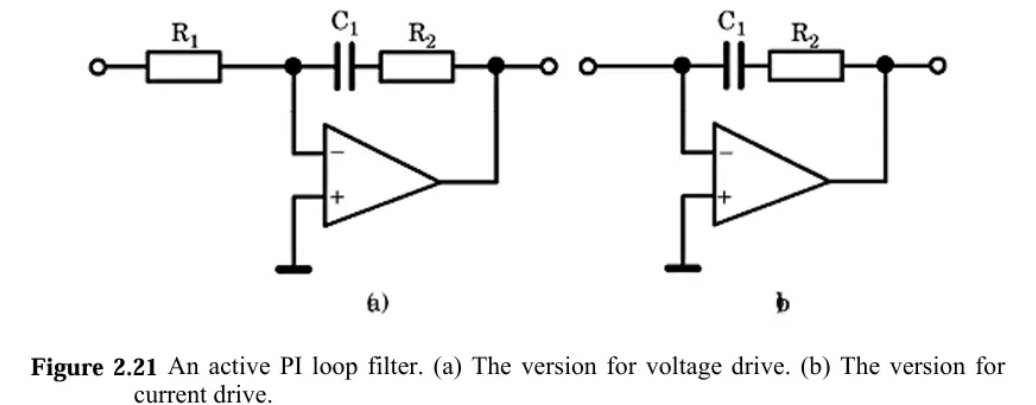
但现在目前绝大部分CPPLL都是使用无源滤波器，主要是因为噪声小，无源滤波器只有热噪声，并且功耗低，而有源滤波器中的运放噪声不仅包含热噪声，电源噪声，还有闪烁噪声，功耗还高。下面是PFD/CP 和无源滤波器的示意图。来自文献3。

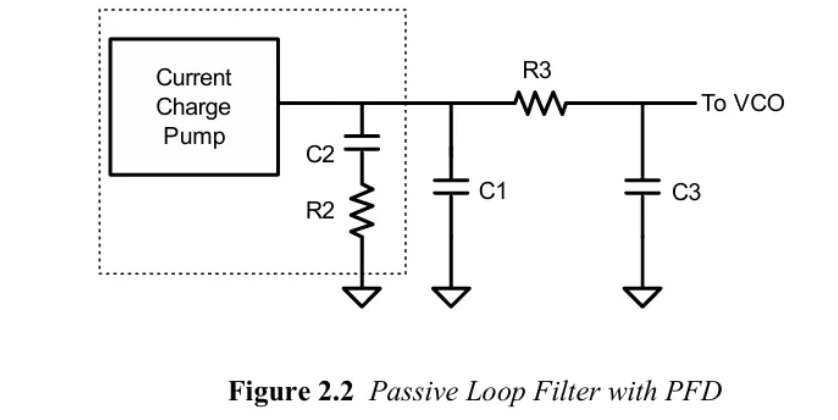
但是这个无源的滤波器有一个缺点，就是比例调节和积分调节合并在一起，不能单独调节。所以出现了一些双路径的CPPLL，比如一篇2002年的JSSC（文献4）的电路示意图

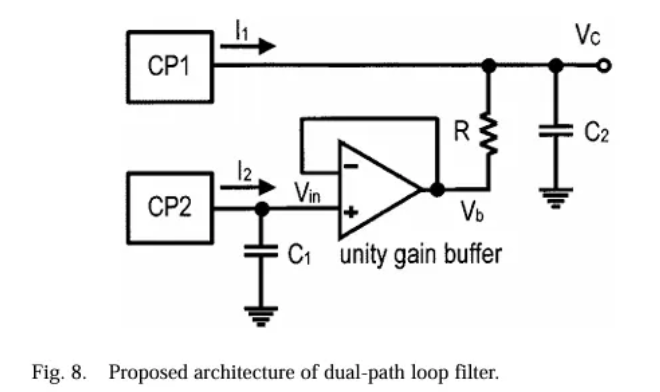
⑤分频器。在PID的那张示意图中并没有出现分频器。但在PLL中常常出现，由于VCO输出频率高于晶振，因此分频器是有必要的。

扩展到数字锁相环

既然分析了CPPLL是如何实现的，那同理数字锁相环也很好扩展。

振荡器需要的是数字输入控制，那么就是数控振荡器（DCO）

相位误差也需要转换为数字信号，所以要实现一个时间数字转换器（TDC），其实我觉得与相位数字转换器是一个意思

PI控制器，在数字域中，乘法和加法都是很好实现的，而且也不存在噪声，也就不需要像模拟锁相环一样考虑分开和不分开了

但数字锁相环会有一个问题是，TDC的量化噪声和小数spur。这都是需要考量的。下面给出一个数字锁相环的示意图，来源于文献5

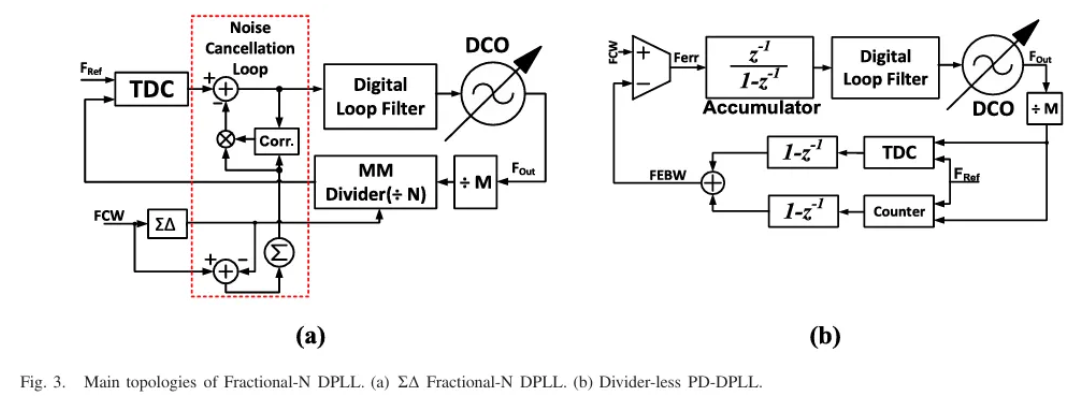
刚才讲到模拟锁相环会将比例路径和积分路径分开，但运算放大器噪声大，所以也有人提出混合型的路径，一个路径用CP，一个路径用TDC实现，如下图所示。来源于文献6

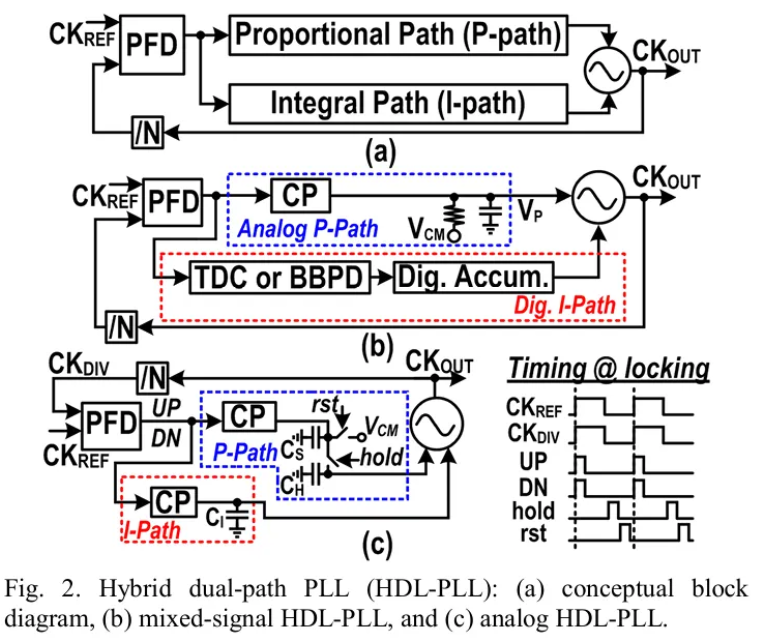
文献都可下载，见我的公众号20251007文件夹。

参考文献

①APCC2015.A wide Frequency PLL-less Clock Generator with Fast Intermittent Operation for Low-Power Wearable Medical Applications

②Roland Best. Phase-Locked Loops Design, simulation, and Applications. sixth version

③Dean Banerjee. PLL performance, simulation, and Design.

④JSSC2002.A fully Integrated CMOS Frequency Synthesizer With Charge-Averaging Charge Pump and Dual-Path Loop Filter for PCS- and Cellular-CDMA Wireless Systems

⑤JSSC2017.A 50–66-GHz Phase-Domain Digital Frequency Synthesizer With Low Phase Noise and Low Fractional Spurs

⑥ICSICT2020.Design of High-performance Phase-Locked Loop Using Hybrid Dual-Path Loop Architecture :an  Overview  (Invited paper)