✳ 我们如何去评估一个信号的频率呢？

从感觉上，总感觉加sdm去实现小数分频不太靠谱，明明一会2分频，一会3分频，怎么平均一下就实现了2.5分频呢？

我其实挺好奇第一个人为什么会想到用平均去实现小数分频的。

回过头来想，现实中的电路，即便VCO产生相噪特别低的信号，每个周期的时间也会有一些差别，这个时候怎么评估这个VCO的频率呢？对，就是使用平均。

我又查了一下频率的定义，频率指的是单位时间内重复发生的次数。其实这个定义就包含了平均。

这样想的话，有人会用平均去实现小数分频，就不足为奇了。

感慨！还是得从定义出发。常用的定义反而会觉得不熟悉。

❓ 问题来了：组成平均值的序列有这么多，他们有什么区别呢？

举个例子：以2.5为例

正常的小数序列是2.5，2.5，2.5，2.5，2.5…….这样循环

在PLL中，只有整数分频，那如果用整数平均形成2.5的话

可以有 2，3，2，3，2，3，2，3

也可以2，2，3，3，2，2，3，3

加大整数的范围，可以有 1，2，3，4，1，2，3，4这样

那这些序列对分频有什么影响呢？

问题转化为，这些序列对PLL的分频有什么影响？

由上一篇文章知道，由于分频器只在输出上升沿有影响，可以只将相位线性化进行分析。

由于分频器的相位与序列是线性相关的，所以序列的功率谱形状，应该与分频器输出相位的功率谱形状相似，因此，为简化，先考虑序列的功率谱形状。

这里为什么是用功率谱分析呢？因为相位噪声的定义是功率的比值。

✅ 不同的序列功率谱的区别？

1. 正常小数序列①[2.5,2.5,2.5,2.5…..]的功率谱只在载波有能量，其他能量是增加了白噪声。

   
   

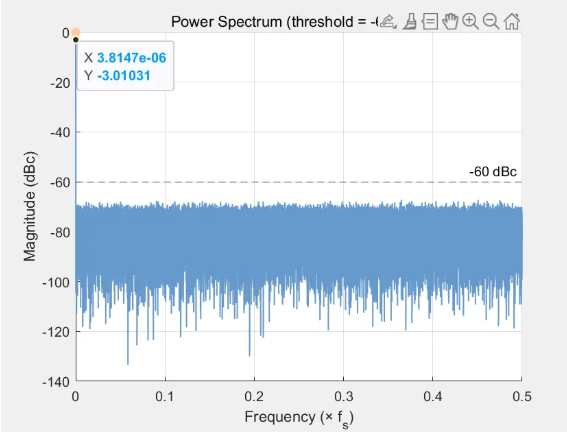
2. 序列②[2,3,2,3,2,3….]在载波和0.5fs处有能量，并且为-13.98dBc。fs为采样频率。

   
   

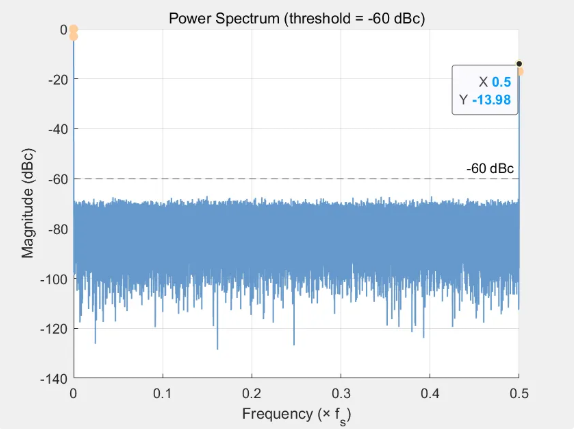
3. 序列③[2,2,3,3,…]在载波和0.25fs处有能量，并且为-13.97dBc

   
   

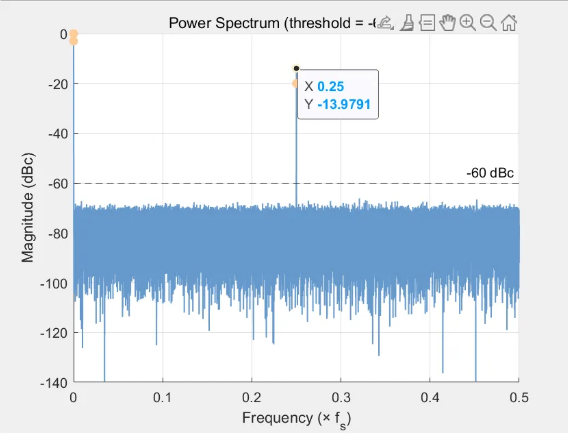
4. 序列[2,2,2,2,2,3,3,3,3,3]在载波和0.1fs，0.3fs，0.5fs处有能量，分别为-14.74dBc，-23.1106dBc，-27.94dBc

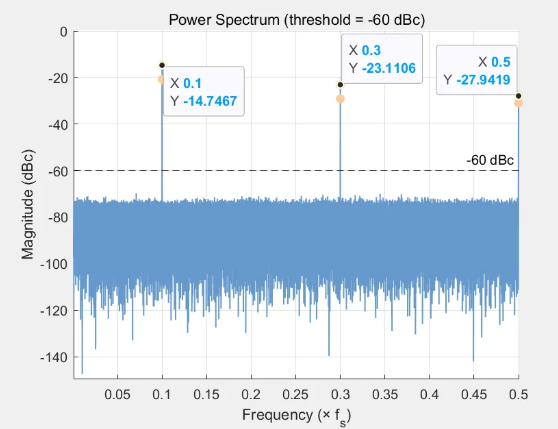
🔁 从上面几个序列的功率谱可以发现几个规律。

一，只有序列①[2.5,2.5,2.5…]是没有杂波的；而其他“求平均”的序列或多或少都会存在杂波。

二，“求平均”的序列产生的杂波分布是与采样频率fs相关的；

二，重复的序列越长，杂波的基频越高，但能量与载波相比会更高；比如序列②[2,3,2,3…]重复的周期是2，而基频是0.5fs，但功率与载波相比-13.9dBc；序列④[2,2,2,2,2,3,3,3,3,3]重复的周期是5，基频是0.1fs，与载波相比是-14.74dBc。

💡 从以上规律可以怎么去实现小数分频？

既然我们产生的序列存在杂波，那不是滤除这些杂波，我们就可以实现性能很好的小数分频了吗？刚好PLL中的环路滤波器是低通滤波器。我们可以把环路滤波器带宽外的杂波全部滤除。

但是，我们的杂波分布不一定在环路滤波器外，我们可以怎么做？

第一，因为杂波分布是与采样频率fs相关，我们可以直接提高fs，这样杂波分布也会更高频，提高fs，也就是降低分频比。

第二，由于杂波的分布与序列相关，可以找到一种算法，将低频的杂波能量小一点，然后将高频的杂波能量大一点，这就是噪声整形（noise shaping）。而sigma-delta调制器实现的就是这样的一个算法。我们常说的将量化噪声推向高频，就是这个意思。

📎 后续

后续研究一下sigma-delta 调制器为什么会产生噪声整形的效果。