日志
同样是三阶结构,为何HK-MASH比MASH111“静”得多?
热度 1| ||
前言
上一篇文章说到除了dither,还有什么方式去抑制SDM的spur?,不使用dither,可以通过不同的方式去延长MASH结构的周期长度。其中有一种变形结构HK-MASH能延长传统MASH结构的序列周期,并且底噪会比加dither的MASH111结构好,那么,这是如何想到这种结构的呢?
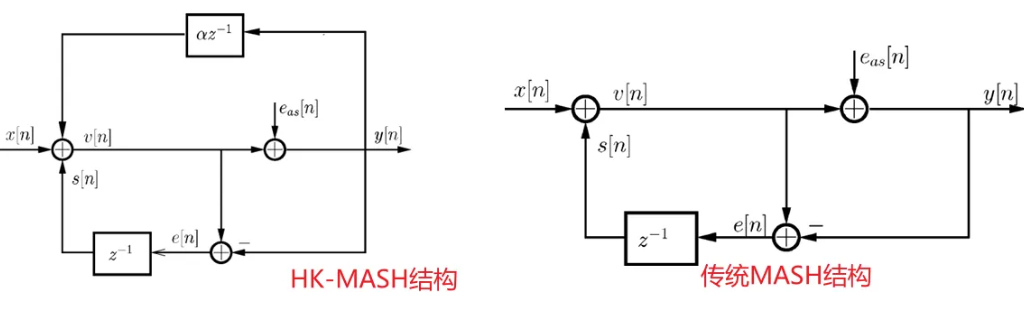
直觉入手
首先,还是需要从我们能看到的入手,先分析一下传统MASH结构一阶的SDM是如何循环的
可以看两个例子
①输入 1/10。序列为1,2,3,4,5,6,7,8,9,0循环;只有一个循环;长度为10
②输入2/10。序列为2,4,6,8,0或者1,3,5,7,9循环;有两个循环;长度为5
可以发现,不同的输入,输出的序列会有不同的序列长度,以及不同的循环个数。那序列长度和循环个数由什么决定呢?
这个数论中模运算可以给出答案
输入为固定分数p/q。则序列长度为L=q/gcd(p,q),其中gcd(p,q)是p和q的最大公约数。
循环个数为gcd(p,q)
| 输入分数p/q | gcd(p,q) | 周期长度L=q/gcd(p,q) | 循环次数=gcd(p,q) | 说明 |
|---|---|---|---|---|
| 1/10 | 1 | 10 | 1 | 最长周期 |
| 2/10 | 2 | 5 | 2 | 两个周期为5的循环 |
| 3/10 | 1 | 10 | 1 | 最长周期 |
| 4/10 | 2 | 5 | 2 | 两个周期为5的循环 |
| 5/10 | 5 | 2 | 5 | 五个周期为2的循环 |
我们可以发现,当循环次数为1的时候,周期长度是最长的,因为遍历了分母的所有数字。有多个循环的长度自然就少了。那很自然,我们可不可以把所有循环都用上呢?
如何把所有循环都用上?
我们是不是可以,在循环一个之后,再循环下一个周期呢。比如2/10,有两个周期,2,4,6,8,0,和1,3,5,7,9。那我可不可以再第一个周期为0的时候,下一个循环是1,3,5,7,9中任意一个数字,这样就能形成2,4,6,8,0,1,3,5,7,9,这样的长度为10的序列了。
那如何打破这种循环呢?其实很简单,就是在你想跳到下个周期的时候,改变分数的分子或者分母。
在这里HK-MASH选择改变了分数的分子,至于改变小数的分母困不困难,有兴趣的话可以自己研究,说不定又是一篇论文。
那么,问题又来了,对于这么多不同的输入,想要改变分数的分子,那我应该改变多少,怎么改变呢?我可以在一个周期序列结束之后,稍微改变分子,比如说2,4,6,8,0的时候加3,这个时候就跳到3了,循环就变成2,4,6,8,0,3,5,7,9,1,4这样循环周期一下子就变长了,从长度5变成了长度10。这个就是HK-MASH的基本思想。
而HK-MASH的示意图中的a,是控制分子改变的多少,对于不同的分母,会有不同的系数。
比如,在2/10这个输入,a=1,循环的周期就是2,4,6,8,0,3,5,7,9,1,4,6,8,0,3,周期长度变为了9,远远大于2/10的5。
HK MASH结构的缺点
①平均值会有误差
从上面的序列,我们发现,我们在累加的过程中增加了数值,所以平均值会随系统中的数值偏移,具体偏移了多少呢?请看HK-MASH的系统函数

相当于输出是输入的(1-α)倍,这里的α是经过归一化的,假设mod为M,电路中反馈系数是a,那么α=a/M,比如论文中采用的M=2^19,a=1,那么输出是输入的(1-1/2^19)倍,会有些误差,但不是特别大。
这个系统函数相当于在原来MASH结构又乘了一个极点为α的系统,α接近原点,因此稳定性没有问题。
均值误差如何解决?
如果要达到均值和原来一样,那么输入需要乘(1-α(1/z)),论文中的做法是在输出乘一个系统函数,但是,输出范围就会从MASH的[-3,4]变为更大的范围了,在PLL中,这可能会影响鉴相器的工作范围。并且比较难实现,系统函数中的α是一个归一化的值,是一个小数。

另一个方法就是在输入分频比的时候,通过手动计算一下,按比例缩小,这个对于输入是一个固定分频的PLL是可以的。
②反馈系数a的硬件实现
在论文中,a有可能是1,3,5,7,9等等系数,如果是1的话,比较好实现,但如果是3,5,7,9等数字,这个会影响到SDM的工作频率,实现起来会更复杂,可能需要更多的流水线(pipeline)去实现更高的频率。
HK MASH和传统MASH的simulink对比
我们可通过仿真看看HK MASH结构的性能,SDM为24bit,输入为0.5
一、不加dither的MASH 1 1 1结构
①图1为功率谱,明显出现spur;
②图二为前1000个SDM的时域信号,序列均值为0.499985,存在一些误差;
③图三为输出序列的分布,可以看到只有[-1,2]的取值,并没有-3,-2,3,4这些值;
④图四是不同计算方式的功率谱对比

二,加dither的MASH 1 1 1功率谱仿真图
①图1为功率谱,没有spur,近似斜率为56.67dB/dec;
②图二为前1000个SDM的时域信号,序列均值为0.5000065000,误差较小;
③图三为输出序列的分布,可以分布[-3,4],并且服从高斯分布;
④图四是不同的计算功率谱的对比

三,HK-MASH结构仿真图
①图1为功率谱,没有spur,近似斜率为57.89dB/dec,比MASH 1 1 1的大些;
②图二为前1000个SDM的时域信号,序列均值为0.4999995,存在一些误差,误差比MASH大(这里输入并没有做处理);
③图三为输出序列的分布,可以分布[-3,4],并且服从高斯分布;
④图四是不同的计算功率谱的对比

四,带dither的MASH 1 1 1和HK MASH比较
图中显示,确实如论文所说,HK MASH会比MASH结构底噪好一些

思考:在PLL应用中是否可使用呢?
对于PLL,由于底噪比MASH 1 1 1结构的更低,HK-MASH结构的SDM确实值得尝试一下,不过需要考虑硬件实现方面的问题,由于多了一个反馈回路,时序裕量可能会更严格。至于平均值的误差,完全可以靠外部实现。
文献
①TCAS Ⅰ2007.Maximum Sequence Length MASH Digital Delta-Sigma Modulators

 /1
/1 

 eetop公众号
eetop公众号 创芯大讲堂
创芯大讲堂 创芯人才网
创芯人才网