3-Stage Nested Miller Compensation 的经典结论推到来自于Huijsing 的 "Frequency Compensation Techniques For Low-Power Operational Amplifiers" 

书中利用三阶巴特沃兹函数系数 （1，2，2，1）求解系统函数的系数，推导出相位裕度60°时 

这个结果很简洁，但推到过程缺乏直观性，不利于调节电路时参数的选择。（也有书建议比例是 1/3， 1/9）

为了方便直观理解和电路参数调节，可以分别考虑两个反馈环路。

1. 只考虑内环，gm2, gm1,Cm1

   
   

   这是简单的两级Miller补偿，高频极点在 p'=gm1/Cl,   单位增益带宽gm2/Cm1=1/2*p'时有大约60°相位裕度。

2. 考虑外环

   
   

电路可以近似等效为上两图（当Cm1>>Cp)，“Design of Three-Stage Class-AB 16 ohm Driver Capable of Handling Wide Range
of Load Capacitance"   Appendix A 有理论推导，过程比较简单，这里不做赘述。

gm2,gm1,Cm1的单位反馈闭环的3dB带宽等于开环的单位增益带宽gm2/Cm1.    也就是说整个系统有个高频极点在gm2/Cm1. 主极点在gm3的输出端(miller effect), 单位增益带宽在 gm3/Cm2.   当 gm3/Cm2=1/2*gm2/Cm1=1/4*gm1/Cl时，可以获得60°相位裕度。

这样的直观解法可获得和Hujsing相同的结果，对实际的电路参数调节更有帮助。

NMC对极点的变化图：

y

NMC的缺点是带宽受限，尤其是当负载电容偏大，p1'=gm1/CL较小时。系统带宽只有其1/4.

DFCFC结构通过在第二级引入零点拓宽了后两级的单位增益带宽，提高了系统的带宽，依然使用上述方法分析。参考论文 “Three-Stage Large Capacitive Load Amplifier with
Damping-Factor-Control Frequency Compensation” JSSC Feb 2000.  为了和论文结论方便比对，交换了gm1, gm3的命名。

gm4, Cm2,R4 构成了damping circuit. 可等效为电阻和电容串联，这里不做具体推导（求反馈系统的输入电阻）。 

1/gm4 和gm4*R4*Cm2形成了一个零点，补偿了rds2,gm4*R4*Cm2形成的低频极点的相移，在系统单位增益带宽处表现为电阻1/gm4,高频极点 gm4/Cp .  在此频率下进一步简化电路

对比论文公式：

当CL>>Cp2时

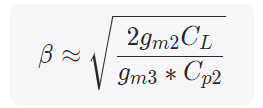
上述分析的结果和论文结果近似。